La geometría, del griego geo (tierra) y metrón (medida), es una rama de la matemática que se ocupa de las propiedades de las figuras geométricas en el plano o el espacio, como son: puntos, rectas, planos, polígonos, poliedros, paralelas, perpendiculares, curvas, superficies, etc. Sus orígenes se remontan a la solución de problemas concretos relativos a medidas y es la justificación teórica de muchos instrumentos, por ejemplo el compás, el teodolito y el pantógrafo. Tiene su aplicación práctica en física, mecánica, cartografía, astronomía, náutica, topografía, balística, etc. También da fundamento teórico a inventos como el sistema de posicionamiento global (en especial cuando se la considera en combinación con el análisis matemático y sobre todo con las ecuaciones diferenciales) y es útil en la preparación de diseños (justificación teórica de la geometría descriptiva, del dibujo técnico e incluso en la fabricación de artesanías).
angulos llanos
Un ángulo llano cambia la dirección para apuntar en la dirección contraria, se ve como una línea recta.
Su medida es de 180° (media revolución, o dos ángulos rectos).
Angulo Complementario
Los ángulos complementarios son aquellos cuya suma de medidas es 90º (grados sexagesimales). Si dos ángulos complementarios son adyacentes, los lados no comunes de los dos forman un ángulo recto.
Así, para obtener el ángulo complementario de α que tiene una amplitud de 70°, se restará α de 90°:Estadistica Inductiva
La estadística inductiva o inferencia estadística es la parte de la estadística que generaliza los resultados muestrales para inferir las características de una población, formulando hipótesis sobre la misma. Tiene por objeto tanto el conseguir la descripción de las poblaciones observadas a través de sus muestras, como el poder ajustar y contrastar aquellos modelos que dan a conocer el proceso formativo de determinadas poblaciones.
Estadistica Descriptiva
La estadística descriptiva es una gran parte de la estadística que se dedica a analizar y representar los datos. Este análisis es muy básico. Aunque hay tendencia a generalizar a toda la población, las primeras conclusiones obtenidas tras un análisis descriptivo, es un estudio calculando una serie de medidas de tendencia central, para ver en qué medida los datos se agrupan o dispersan en torno a un valor central.
Sumatorios
El sumatorio o la sumatoria es un operando matemático que permite representar sumas de muchos sumandos, n o incluso infinitos sumandos, se expresa con la letra griega sigma ( Σ ), y se define como :
Esto se lee: "Sumatorio sobre i, desde m hasta n, de x sub-i", o bien "sumatoria de i, desde i = m a n, de x sub-i"
La variable i es el índice de suma al que se le asigna un valor inicial llamado límite inferior, m. La variable i recorrerá los valores enteros hasta alcanzar el límite superior, n. Necesariamente debe cumplirse que:
 =
= 
-
-
-
-
-
-
-
-
-
- β = 90° – 70º = 20º
-
-
-
-
-
-
-
-
- el ángulo β (beta) es el complementario de α (alfa).
- 360 grados sexagesimales equivalen a 2π radianes, o 400 grados centesimales.
BicecTriz
La bisectriz de un ángulo es la recta que lo divide en dos partes iguales. Es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia) de las semirrectas de un ángulo.
Características
El punto de la bisectriz es equidistante a los dos lados (rectas) del ángulo. Recíprocamente, dos rectas, al cruzarse, determinan cuatro ángulos y cada uno de ellos define una bisectriz. Estas bisectrices resultan ser el lugar geométrico de los puntos equidistante.
En la figura, la bisectriz interior al ángulo xOy (en amarillo) es (sz'), y la exterior es (ww'). Se cortan formando un ángulo recto. En efecto, si llamemos a la medida de xOz, y b la de yOw, observamos que 2a + 2b es la medida del ángulo xOx' , que es plano. Dividimos por 2: zOw mide a + b = 90º.
Las tres bisectrices de los ángulos internos de un triángulo se cortan en un único punto, que equidista de los lados. Este punto se llama el incentro del triángulo y es el centro de la circunferencia inscrita al triángulo. Esta circunferencia es tangente a cada uno de los lados del triángulo.
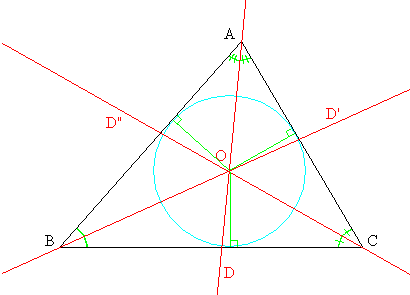
Demostración: Dos bisectrices del triángulo no pueden ser paralelas. Sea O la intersección de las bisectrices D y D' (ver figura). Como O pertenece a D, es equidistante de las rectas (AB) y (AC). Como O pertenece a D', entonces también equidista de las rectas (AB) y (BC). Por transitividad de la igualdad, es equidistante de (AC) y (BC), y pertenece a la bisectriz (interior) del ángulo C, es decir a D". Al ser equidistante a los tres lados. Se sigue que la circunferencia cuyo radio sea justamente la distancia común del punto O a los lados del triángulo es tangente a cada uno de los lados.
Cilindro RectoUn cilindro, en geometría, es la superficie formada por los puntos situados a una distancia fija de una línea recta dada, el eje del cilindro. Como superficie de revolución, se obtiene mediante el giro de una recta alrededor de otra fija llamada eje de revolución.
El sólido encerrado por esta superficie y por dos planos perpendiculares al eje también se llama cilindro.
En geometría diferencial, un cilindro se define de forma general como cualquier superficie reglada generada por una familia uniparametrica de líneas paralelas.
AlGEBRA
YupanaUn cilindro, en geometría, es la superficie formada por los puntos situados a una distancia fija de una línea recta dada, el eje del cilindro. Como superficie de revolución, se obtiene mediante el giro de una recta alrededor de otra fija llamada eje de revolución.
El sólido encerrado por esta superficie y por dos planos perpendiculares al eje también se llama cilindro.
En geometría diferencial, un cilindro se define de forma general como cualquier superficie reglada generada por una familia uniparametrica de líneas paralelas.
Termino aLgebraico
ECUACION
Una ecuación es una igualdad entre dos expresiones algebraicas, denominadas miembros, en las que aparecen valores conocidos o datos, y desconocidos o incógnitas, relacionados mediante operaciones matemáticas. Los valores conocidos pueden ser números, coeficientes o constantes; y también variables cuya magnitud se haya establecido como resultado de otras operaciones. Las incógnitas, representadas generalmente por letras, constituyen los valores que se pretende hallar. Por ejemplo, en la ecuación:
La letra x representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. Resolver una ecuación es encontrar los valores de las incógnitas que la satisfacen, y se llama solución de una ecuación a cualquier valor de dichas variables que cumpla la igualdad planteada. Para el caso dado, la solución es:
Todo problema matemático puede expresarse en forma de una o más ecuaciones. Sin embargo no todas las ecuaciones tienen solución, ya que es posible que no exista ningún valor de la incógnita que haga cierta una igualdad dada. También puede ocurrir que haya varios o incluso infinitos conjuntos de valores que la satisfagan.
En el caso de que todo valor posible de la incógnita haga cumplir la igualdad, la expresión se llama identidad. Si en lugar de una igualdad se trata de una desigualdad entre dos expresiones matemáticas, se denominará inecuación. Una ecuación funcional es aquella en la que algunas de las constantes y variables que intervienen no son realmente números sino funciones; y si en la ecuación aparece algún operador diferencial se llama ecuación diferencial.
POtencia
El término Potencia (del latín potentĭa: "poder, fuerza") puede designar a:
- Potencia eléctrica: cantidad de energía eléctrica o trabajo que se transporta o que se consume en una determinada unidad de tiempo.
- Potencia (en óptica): inverso de la distancia focal de una lente o espejo.
- Potencia acústica: la cantidad de energía por unidad de tiempo emitida por una fuente determinada en forma de ondas sonoras.
- Etapa de potencia: un amplificador de audio.
- Potencia de Planck: unidad de medida.
- Potencia: producto que resulta al multiplicar una cantidad o expresión por sí misma una o más veces.
- Potenciación: multiplicación de varios factores iguales de un anillo multiplicativo.
- Potencia de un conjunto: operación abstracta con conjuntos.
- Conjunto potencia: dado un conjunto S, el conjunto potencia o conjunto de partes de S.
- Potencia de un punto (en geometría): potencia respecto de una circunferencia.
- tamaño:
- Pequeña potencia
- Mediana potencia o potencia intermedia.
- Gran potencia
- Superpotencia: históricamente, la Unión Soviética y los Estados Unidos fueron superpotencias entre 1945 y 1991.
- Superpotencias emergentes
- Hiperpotencia
- Potencia regional: la que limita su capacidad de influencia a un entorno geopolítico regional (en:Regional power en la wikipedia en inglés).
- Potencia mundial: la que tiene una capacidad de influencia a nivel mundial.
- Potencias históricas o historia de las grandes potencias (Historical powers en la wikipedia en inglés o istoire des grandes puissances en la wikipedia en francés).
- Potencia económica (véase país desarrollado, país recientemente industrializado, BRIC, G8, G20, OCDE, etc.)
unidades regulares:
El grupo de Regulares pertenece a las fuerzas militares españolas creadas en 1911, en África y con personal indígena, cuya organización fue: un Tabor (o batallón) de Infantería de cuatro compañías más un escuadrón de caballería, que se ampliaron al año siguiente a dos Tabores de Infantería más un Tabor de Caballería.
El grupo de Regulares pertenece a las fuerzas militares españolas creadas en 1911, en África y con personal indígena, cuya organización fue: un Tabor (o batallón) de Infantería de cuatro compañías más un escuadrón de caballería, que se ampliaron al año siguiente a dos Tabores de Infantería más un Tabor de Caballería.
teorema de pitagoras
El Teorema de Pitágoras establece que en un triángulo rectángulo el cuadrado de la longitud de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de las longitudes de los dos catetos (los dos lados menores del triángulo rectángulo: los que conforman el ángulo recto). Si un triángulo rectángulo tiene catetos de longitudes
 y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que: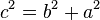
Historia de la estadistica
Los comienzos de la estadística pueden ser hallados en el antiguo Egipto, cuyos faraones lograron recopilar, hacia el año 3050 antes de Cristo, prolijos datos relativos a la población y la riqueza del país. De acuerdo al historiador griego Heródoto, dicho registro de riqueza y población se hizo con el objetivo de preparar la construcción de las pirámides. En el mismo Egipto, Ramsés II hizo un censo de las tierras con el objeto de verificar un nuevo reparto.
En el antiguo Israel la Biblia da referencias, en el libro de los Números, de los datos estadísticos obtenidos en dos recuentos de la población hebrea. El rey David por otra parte, ordenó a Joab, general del ejército hacer un censo de Israel con la finalidad de conocer el número de la población.
También los chinos efectuaron censos hace más de cuarenta siglos. Los griegos efectuaron censos periódicamente con fines tributarios, sociales (división de tierras) y militares (cálculo de recursos y hombres disponibles). La investigación histórica revela que se realizaron 69 censos para calcular los impuestos, determinar los derechos de voto y ponderar la potencia guerrera.
Pero fueron los romanos, maestros de la organización política, quienes mejor supieron emplear los recursos de la estadística. Cada cinco años realizaban un censo de la población y sus funcionarios públicos tenían la obligación de anotar nacimientos, defunciones y matrimonios, sin olvidar los recuentos periódicos del ganado y de las riquezas contenidas en las tierras conquistadas. Para el nacimiento de Cristo sucedía uno de estos empadronamientos de la población bajo la autoridad del imperio.
Durante los mil años siguientes a la caída del imperio Romano se realizaron muy pocas operaciones Estadísticas, con la notable excepción de las relaciones de tierras pertenecientes a la Iglesia, compiladas por Pipino el Breve en el 758 y por Carlomagno en el 762 DC. Durante el siglo IX se realizaron en Francia algunos censos parciales de siervos. En Inglaterra, Guillermo el Conquistador recopiló el Domesday Book o libro del Gran Catastro para el año 1086, un documento de la propiedad, extensión y valor de las tierras de Inglaterra. Esa obra fue el primer compendio estadístico de Inglaterra.
Aunque Carlomagno, en Francia; y Guillermo el Conquistador, en Inglaterra, trataron de revivir la técnica romana, los métodos estadísticos permanecieron casi olvidados durante la Edad Media.
Durante los siglos XV, XVI, y XVII, hombres como Leonardo de Vinci, Nicolás Copérnico, Galileo, Neper, William Harvey, Sir Francis Bacon y René Descartes, hicieron grandes operaciones al método científico, de tal forma que cuando se crearon los Estados Nacionales y surgió como fuerza el comercio internacional existía ya un método capaz de aplicarse a los datos económicos.
Para el año 1532 empezaron a registrarse en Inglaterra las defunciones debido al temor que Enrique VII tenía por la peste. Más o menos por la misma época, en Francia la ley exigió a los clérigos registrar los bautismos, fallecimientos y matrimonios. Durante un brote de peste que apareció a fines de la década de 1500, el gobierno inglés comenzó a publicar estadísticas semanales de los decesos. Esa costumbre continuó muchos años, y en 1632 estos Bills of Mortality (Cuentas de Mortalidad) contenían los nacimientos y fallecimientos por sexo. En 1662, el capitán John Graunt usó documentos que abarcaban treinta años y efectuó predicciones sobre el número de personas que morirían de varias enfermedades y sobre las proporciones de nacimientos de varones y mujeres que cabría esperar. El trabajo de Graunt, condensado en su obra Natural and Political Observations...Made upon the Bills of Mortality (Observaciones Políticas y Naturales ... Hechas a partir de las Cuentas de Mortalidad), fue un esfuerzo innovador en el análisis estadístico.
Por el año 1540 el alemán Sebastián Muster realizó una compilación estadística de los recursos nacionales, comprensiva de datos sobre organización política, instrucciones sociales, comercio y poderío militar. Durante el siglo XVII aportó indicaciones más concretas de métodos de observación y análisis cuantitativo y amplió los campos de la inferencia y la teoría Estadística.
Los eruditos del siglo XVII demostraron especial interés por la Estadística Demográfica como resultado de la especulación sobre si la población aumentaba, decrecía o permanecía estática.
En los tiempos modernos tales métodos fueron resucitados por algunos reyes que necesitaban conocer las riquezas monetarias y el potencial humano de sus respectivos países. El primer empleo de los datos estadísticos para fines ajenos a la política tuvo lugar en 1691 y estuvo a cargo de Gaspar Neumann, un profesor alemán que vivía en Breslau. Este investigador se propuso destruir la antigua creencia popular de que en los años terminados en siete moría más gente que en los restantes, y para lograrlo hurgó pacientemente en los archivos parroquiales de la ciudad. Después de revisar miles de partidas de defunción pudo demostrar que en tales años no fallecían más personas que en los demás. Los procedimientos de Neumann fueron conocidos por el astrónomo inglés Halley, descubridor del cometa que lleva su nombre, quien los aplicó al estudio de la vida humana. Sus cálculos sirvieron de base para las tablas de mortalidad que hoy utilizan todas las compañías de seguros.
Durante el siglo XVII y principios del XVIII, matemáticos como Bernoulli, Francis Maseres, Lagrange y Laplace desarrollaron la teoría de probabilidades. No obstante durante cierto tiempo, la teoría de las probabilidades limitó su aplicación a los juegos de azar y hasta el siglo XVIII no comenzó a aplicarse a los grandes problemas científicos.
Godofredo Achenwall, profesor de la Universidad de Gotinga, acuñó en 1760 la palabra estadística, que extrajo del término italiano statista (estadista). Creía, y con sobrada razón, que los datos de la nueva ciencia serían el aliado más eficaz del gobernante consciente. La raíz remota de la palabra se halla, por otra parte, en el término latino status, que significa estado o situación; Esta etimología aumenta el valor intrínseco de la palabra, por cuanto la estadística revela el sentido cuantitativo de las más variadas situaciones.
Jacques Quételect es quien aplica las Estadísticas a las ciencias sociales. Este interpretó la teoría de la probabilidad para su uso en las ciencias sociales y resolver la aplicación del principio de promedios y de la variabilidad a los fenómenos sociales. Quételect fue el primero en realizar la aplicación práctica de todo el método Estadístico, entonces conocido, a las diversas ramas de la ciencia.
Entretanto, en el período del 1800 al 1820 se desarrollaron dos conceptos matemáticos fundamentales para la teoría Estadística; la teoría de los errores de observación, aportada por Laplace y Gauss; y la teoría de los mínimos cuadrados desarrollada por Laplace, Gauss y Legendre. A finales del siglo XIX, Sir Francis Gaston ideó el método conocido por Correlación, que tenía por objeto medir la influencia relativa de los factores sobre las variables. De aquí partió el desarrollo del coeficiente de correlación creado por Karl Pearson y otros cultivadores de la ciencia biométrica como J. Pease Norton, R. H. Hooker y G. Udny Yule, que efectuaron amplios estudios sobre la medida de las relaciones.
Los progresos más recientes en el campo de la Estadística se refieren al ulterior desarrollo del cálculo de probabilidades, particularmente en la rama denominada indeterminismo o relatividad, se ha demostrado que el determinismo fue reconocido en la Física como resultado de las investigaciones atómicas y que este principio se juzga aplicable tanto a las ciencias sociales como a las físicas.
Tanto por ciento
Calcular el tanto por ciento, t %, de una cantidad A consiste en encontrar una cantidad B de forma que A y B estén en la misma proporción que 100 y t.Así, si el t % de una cantidad A es otra cantidad B, se verifica:
Por tanto, sin tener más que dos de estos datos se puede averiguar el tercero.
Decir que el t % de cierto colectivo (cuya representación debe ser numérica) verifica algo, significa que de cada 100 individuos de ese colectivo, t cumplen dicha condición.
Así, por ejemplo, si se dice que «el 25 % de las personas que forman un Parlamento son de la oposición», se está diciendo que de cada 100 parlamentarios, 25 son de la oposición.
Si hay 100 parlamentarios, 25 son de la oposición
Si hay 300 parlamentarios, 75 son de la oposición
Ejercicio: cálculo de tantos por ciento
1. ¿Cuál es el 25 % de 480?
Resolución:
En este caso A = 480 y t = 25. Se debe calcular B.
Un término algebraico consta de las siguientes partes:
Ejemplo: - Signo. Puede ser positivo (+), o negativo (-).
- Coeficiente. En el producto de dos o más factores, cualquiera de ellos puede llamarse coeficiente de los otros factores
| En 7ab2c ; | 7 es coeficiente de ab2c |
| a es coeficiente de 7b2c | |
| b2 es coeficiente de 7ac | |
| c es coeficiente de 7ab2 |
En general, se le llama coeficiente a una constante (con todo y signo), que es un factor de las variables de cualquier término algebraico.
- Variable (o parte literal). Cantidad generalizada.
- Exponente. Es el número de veces que se multiplicará la cantidad generalizada o variable, por sí misma.
Ejemplos:
| a) -2x2; | Signo: negativo |
| Coeficiente: -2 | |
| Variable: x | |
| Exponente: 2 | |
| b) ax2y3; | Signo: positivo |
| Coeficiente: a | |
| Variables: x , y | |
Exponentes: 2 (de la x) 3 (de la y) |

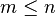
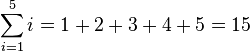

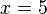
No hay comentarios:
Publicar un comentario